


Next: 12. The Proof System
Up: 2. User's Guide
Previous: 10. Quasi-Constructors
Subsections
11. Theory Ensembles
Much of mathematics deals with the study of structures such as
monoids, fields, metric spaces, or vector spaces, which consist of an
underlying set S, some distinguished constants in S, and
one or more functions on S. In IMPS, an individual structure of
this kind can be easily formalized as a theory. For example, the
IMPS theory for monoids is specified by two def-forms:
(def-language MONOID-LANGUAGE
(embedded-languages h-o-real-arithmetic)
(base-types uu)
(constants
(e uu)
(** (uu uu uu))))
(def-theory MONOID-THEORY
(component-theories h-o-real-arithmetic)
(language monoid-language)
(axioms
(associative-law-for-multiplication-for-monoids
"forall(z,y,x:uu, x**(y**z)=(x**y)**z)")
("forall(x:uu,x**e=x)")
("forall(x:uu,e**x=x)")))
In the mathematical syntax, the sort uu is written U
and the constants e, star* are written
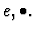
Notice that the theory of a monoid as presented here is suitable for
concept formulation and proof in a single monoid. Here are some examples:
- One can prove uniqueness of the multiplicative identity:
- A sequential product operator for sequences can be defined as the least
solution of
- One can easily prove
 satisfies
satisfies
- An monoid endomorphism (i.e., a self homomorphism) can be
defined by the predicate
However, there is no way to talk about monoid homomorphisms between
different monoids.
Nevertheless, it is possible to produce a suitable theory in IMPS in
which a general notion of monoid homomorphism can be defined. To do so
requires at the very least a theory with two possibly distinct
monoids. In general, multiple instances of structures can be dealt
with in IMPS in two ways:
- In one approach, we first formalize set theory as an IMPS theory. This can be
done by treating Set as a primitive sort and the membership
relation
 as a primitive function symbol. It is then
possible to define a structure of a particular kind by a predicate on
Set. For instance, a monoid is any object in Set of the
form
as a primitive function symbol. It is then
possible to define a structure of a particular kind by a predicate on
Set. For instance, a monoid is any object in Set of the
form
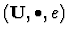 where
where 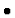 is a binary associative
operation on U for which e is a right and left identity.
is a binary associative
operation on U for which e is a right and left identity.
- The other approach is to create a new theory which is the union
of embedded replicas of a
theory of a single structure. A replica of a theory
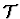 is a
theory
is a
theory
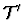 ,
which differs from
,
which differs from 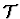 only by an
appropriate renaming of sorts and constants. By an embedding we mean a
theory interpretation which maps distinct sorts and constants to
distinct sorts and constants.
only by an
appropriate renaming of sorts and constants. By an embedding we mean a
theory interpretation which maps distinct sorts and constants to
distinct sorts and constants.
In this section we explain the theory ensemble mechanism, which
implements the second approach above. To illustrate how the machinery
works in the case of a monoid, let us define a new theory, monoid-theory-1 obtained by renaming the sorts and constants of monoid-theory not in h-o-real-arithmetic by affixing the characters
`` _1.''
(def-language MONOID-LANGUAGE-1
(embedded-languages h-o-real-arithmetic)
(base-types uu_1)
(constants
(e_1 uu_1)
(**_1 (uu_1 uu_1 uu_1))))
(def-theory MONOID-THEORY-1
(component-theories h-o-real-arithmetic)
(language monoid-language-1)
(axioms
(associative-law-for-multiplication-for-monoids
"forall(z,y,x:uu_1,
x **_1 (y **_1 z)=(x **_1 y) **_1 z)")
("forall(x:uu_1,x **_1 e_1=x)")
("forall(x:uu_1,e_1 **_1 x=x)")))
Now define monoid-pair as the union of monoid-theory and
monoid-theory-1:
(def-theory MONOID-PAIR
(component-theories monoid-theory monoid-theory-1))
The theory ensemble facility automates these steps and also provides
several bookkeeping devices for keeping track of theories and
interpretations in the ensemble.
A copy of a theory 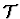 There are four def-forms for building and manipulating theory
ensembles.
There are four def-forms for building and manipulating theory
ensembles.
- def-theory-ensemble. This form is used to build a theory
ensemble from a given theory
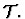 The theory
The theory 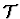 is
called the base theory of the ensemble.
is
called the base theory of the ensemble.
- def-theory-ensemble-multiple. This form is used to build a
theory
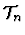 which is the union of n copies of
which is the union of n copies of 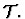
- def-theory-ensemble-instances. This form is used to build
a theory interpretation from a theory multiple
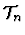 to a given theory.
to a given theory.
- def-theory-ensemble-overloadings. This form establishes overloadings
for the constants defined in
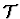 and all the multiples
and all the multiples
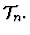
This is the def-form for building
a theory ensemble from an IMPS theory. In the simplest version, the
form requires only one argument, the name of the theory ensemble
which is then identical to the name of the base theory. For example:
(def-theory-ensemble METRIC-SPACES)
Evaluating the def-form builds a theory ensemble also named METRIC-SPACES. In general, three additional keyword arguments are allowed:
- (base-theory theory-name). theory-name is the name
of the base theory of the ensemble. This keyword arguiment is used
when the name of the ensemble is different from that of the base theory.
- (fixed-theories
 .
The presence of this argument
causes IMPS to rename only those sorts and constants which do not
belong to any of the theories
.
The presence of this argument
causes IMPS to rename only those sorts and constants which do not
belong to any of the theories
 when building replicas. The default value of this argument
is the fixed-theories set at the time the form is evaluated.
when building replicas. The default value of this argument
is the fixed-theories set at the time the form is evaluated.
- (replica-renamer proc-name). proc-name is the name
of a procedure of one integer argument, used to name sorts and
constants of theory replicas. The default procedure is to affix an
underscore followed by a nonnegative integer to a name. Most users
should be content to use the default.
Another example which utilizes the fixed-theories option is the theory
ensemble of vector spaces over a field:
(def-theory-ensemble VECTOR-SPACES
(fixed-theories fields))
When a theory ensemble def-form is evaluated, IMPS builds a number of tables, all
of which are initially empty. The table will be filled as multiples
are built. The tables are:
- A table of the theory replicas. The key is an integer
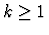 and the entry
is the k-th replica of the base theory.
and the entry
is the k-th replica of the base theory.
- A table of the theory multiples. The key is an integer
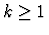 and the entry
is the k-th multiple of the base theory.
and the entry
is the k-th multiple of the base theory.
- A table of canonical interpretations between multiples. The key is a pair of integers
(m, n) with
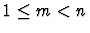 and the corresponding entry is a list of
interpretations from the m-multiple to the n-multiple.
and the corresponding entry is a list of
interpretations from the m-multiple to the n-multiple.
This form requires two arguments, the name of a theory
ensemble and an integer n. For example,
(def-theory-ensemble-multiple metric-spaces 2)
When this form is evaluated, IMPS builds a 2-multiple of the theory
metric-spaces. IMPS automatically names this theory
metric-spaces-2-tuples.
Once the theory metric-spaces-2-tuples is available several important
concepts can be defined. For instance,
(def-constant CONTINUOUS
"lambda(f:[pp_0,pp_1],forall(v:sets[pp_1],
open(v) implies open(inv_image(f,v))))"
(theory metric-spaces-2-tuples))
This form is used to build
interpretations from selected theory multiples and to transport
natively defined constants and sorts from these multiples using these
interpretations. The syntax for this def-form is very elaborate, so
we refer you to Chapter 17 for its general use.
As an example, suppose we wanted to consider the pair consisting of a
normed linear space and the real numbers as a special case of the theory
metric-spaces-2-tuples. One reason for doing this is to make all
the mathematical machinery developed in the abstract theory metric-spaces-2-tuples available in the particular case. This
machinery includes definitions (such as the definition of continuity
for mappings) and theorems (such as the various characterizations of
continuity.)
We would like to build a theory interpretation from metric-spaces-2-tuples to the union of normed-linear-spaces and
h-o-real-arithmetic which is normed-linear-spaces itself,
since normed-linear-spaces is a super-theory of h-o-real-arithmetic. Moreover, we would like
IMPS to translate all the defined sorts and constants in metric-spaces-2-tuples
to normed-linear-spaces.
This can be accomplished by evaluating the form
(def-theory-ensemble-instances METRIC-SPACES
(target-theories
normed-linear-spaces
h-o-real-arithmetic)
(multiples 1 2)
(sorts (pp uu rr))
(constants
(dist "lambda(x,y:uu, norm(x-y))"
"lambda(x,y:rr, abs(x-y))")))
This does two things: First it builds an interpretation from metric-spaces-2-tuples into normed-linear-spaces in which
pp_0 goes to uu.
pp_1 goes to rr.
dist_0 goes to lambda(x,y:uu, norm(x-y).
dist_1 goes to lambda(x,y:rr, abs(x-y)).
Secondly, it translates all the natively defined constants in
metric-spaces and metric-spaces-2-tuples into normed-linear-spaces.
This form takes the following arguments:
- The name of the theory ensemble.
- Any number of integers
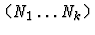
Evaluation of the def-form causes IMPS to overload those constants
natively defined in the theory multiples
 For example:
For example:
(def-theory-ensemble-overloadings metric-spaces 1 2)
This form makes the theory ensemble mechanism manageable to the user.
When the system transports a natively defined constant c from a
theory multiple, it will often give the new constant an unappealing
name. For instance, the name might be very long with several indices
as suffixes. Ideally, one would like to use the same name for all
instances of c, and this is usually possible if the constant is a
function symbol which occurs as an operator of an application. In
this case, the appropriate function symbol may be unambiguously
determined from the sorts of the arguments.
- 1.
- In principle, any theory can be used to build a theory ensemble.
However, the theory ensemble facility is useful only if the following two
conditions on the base theory are met:
- The base theory is fairly general so that there are likely to be
numerous instances of the base theory. Thus it would make little
sense to make a theory with essentially only one model into a theory ensemble.
- There is a need for dealing with at least two distinct
instances of the base theory.
- 2.
- There is a certain amount of overhead in building theory multiples.
This overhead includes building and tabulating theory replicas and
building canonical theory interpretations from the m-multiples to
n-multiples, where m<n. Recall, that there is a canonical
interpretation
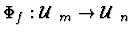 for each
injective map
for each
injective map
There are
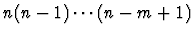 such mappings. This overhead can
become forbidding when the multiples get too large. As a general rule,
multiples of order greater than 4 should be avoided.
such mappings. This overhead can
become forbidding when the multiples get too large. As a general rule,
multiples of order greater than 4 should be avoided.
- 3.
- Before the system builds an n-multiple it checks whether all
j-multiples for j<n already exist, building the missing multiples as needed.



Next: 12. The Proof System
Up: 2. User's Guide
Previous: 10. Quasi-Constructors
System Administrator
2000-07-23