


Next: 18. The Proof Commands
Up: 3. Reference Manual
Previous: 3. Reference Manual
Subsections
17. The IMPS Special Forms
In this chapter, we document a number of user forms for defining and
modifying IMPS objects, for loading sections and files, and for
presenting expressions. We will use the following template to
describe each one of these forms.
- Positional Arguments.
- This is a list of arguments that must
occur in the order given, and must precede the modifier arguments and
the keyword arguments. All IMPS definition forms have a name as
first argument or, a list of names as first argument.
- Modifier Arguments.
- Each modifier argument is a single symbol
called the modifier.
- Keyword Arguments.
- Each keyword argument is a list whose first
element is a symbol called the keyword. Keyword arguments
have one of two forms:
- (keyword arg-component).
- (keyword
 .
.
Note: By default, nearly every special form in this chapter is allowed
to have a keyword argument of the form
where syntax-name is the name of a syntax (e.g., string-syntax or sexp-syntax) which specifies what syntax to
use when reading the form. If this keyword argument is missing, the
current syntax is used when reading the form.
Modifier and keyword arguments can occur in any order.
- Description.
- A brief description of the definition form.
- Remarks:
- Hints or observations that we think you should find useful.
- Examples.
- Some example forms.
def-algebraic-processor
- cancellative. This modifier argument tells the simplifier
to do multiplicative cancellation.
- (language language-name). Required.
- (base spec-forms). Required.
- (exponent spec-forms). Instructs processor how to
simplify exponents if there are any.
- (coefficient spec-forms). Instructs processor how to
simplify coefficients for modules.
In all of the above cases, spec-forms is either a name of an
algebraic processor or is a list with keyword arguments and modifier
arguments of its own. The keyword arguments for spec-forms are:
- (scalars numerical-type).
- (operations
 .
operation-alist is a
list of entries (operation-type operator). operation-type is one of the symbols
.
operation-alist is a
list of entries (operation-type operator). operation-type is one of the symbols + * - / ^ sub zero unit. operator is the name of a constant in the processor language.
The modifier arguments for spec-forms are:
- use-numerals-for-ground-terms.
- commutes.
This form builds an object called a processor for algebraic simplification. Processors are used by IMPS to generate algebraic and order simplification procedures used by the
simplifier for the following purposes:
- To utilize theory-specific information of an algebraic nature in
performing simplification. For example, the expression x+x-x should
simplify to x, or x<x+1 should simplify to true.
- To reduce any expression built from formal constants whose value
can be algebraically computed from the values of the components. Thus
the expression 2+3 should reduce to 5.
In order for simplification to reduce expressions involving only
formal constants (for instance, 2+3), a processor associates such
IMPS terms to executable T expressions involving algebraic procedures
and objects from some data type S. This type is specified by
the scalars declaration of the def-algebraic-processor
form. We refer to this data type as a numerical type. Each
formal constant o which denotes an algebraic function (such as +or -) is associated to an operation f(o) on the data type. This
correspondence is specified by the operations keyword of
processor. Finally, certain terms must be associated to elements of
S. This is accomplished by a predicate and two mappings
constructed by IMPS when the processor is built:
- A predicate that singles out certain terms as numerical
constants. These are called numerical terms. For the processor
used in the theory h-o-real-arithmetic the numerical constants
are those formal constants whose names are rational numbers.
- A function
 which maps certain elements of S to terms.
which maps certain elements of S to terms.
- A function
 which maps certain terms to S.
which maps certain terms to S.
The simplifier uses these functions to reduce
expressions containing numerical terms, according to the following
rule: If f denotes a processor operation, and s,t denote numerical
terms, and o(s,t) is defined, then o(s,t) is replaced by
T(f(o)(N(s),N(t))).
Evaluating a def-algebraic-processor form by itself will not
affect theory simplification in any way. To add algebraic
simplification to a theory, evaluate the form def-theory-processors. It is also important to note that an
algebraic processor can only be installed in the simplifier when
certain theorems generated by the processor are valid in the theory.
(def-algebraic-processor RR-ALGEBRAIC-PROCESSOR
(language numerical-structures)
(base ((scalars *rational-type*)
(operations
(+ +)
(* *)
(- -)
(^ ^)
(/ /)
(sub sub))
use-numerals-for-ground-terms
commutes)))
(def-algebraic-processor VECTOR-SPACE-ALGEBRAIC-PROCESSOR
(language real-vector-language)
(base ((operations
(+ ++)
(* **)
(zero v0))))
(coefficient rr-algebraic-processor))
def-atomic-sort
- sort-name. The name of the atomic sort to be
defined. sort-name also is the name of the newly built definition.
- quasi-sort-string.
- (theory theory-name). Required.
- (usages
 .
.
- (witness witness-expr-string).
This form creates a new atomic sort
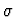 called sort-name from a unary predicate p of sort
called sort-name from a unary predicate p of sort
![$[\sigma,\ast]$](img459.gif) specified by quasi-sort-string and adds a set of
new theorems with usage list
specified by quasi-sort-string and adds a set of
new theorems with usage list
 .
The new atomic sort and new theorems are added to the
theory T named theory-name provided:
.
The new atomic sort and new theorems are added to the
theory T named theory-name provided:
- sort-name is not the name of any current
atomic sort of T or of a structural supertheory of T; and
- the formula
 is known to be a
theorem of T.
is known to be a
theorem of T.
If there is a witness argument, the systems tries to verify
condition (2) by simplifying p(a), where a is the expression
specified by witness-expr-string.
(def-atomic-sort NN
"lambda(x:zz, 0<=x)"
(theory h-o-real-arithmetic)
(witness "0"))
def-bnf
- name. A symbol to serve as the name of the theory that will be
created as a consequence of this def-form. In addition, a second
implementation object with this name is also created; it represents the
BNF definition itself together with the axioms and theorems that it
generates.
- (theory theory-name). Required. The theory that will be
conservatively extended by adding the new datatype. We will refer to
this theory as the underlying theory.
- (base-type type-name). Required. The name of the new data
type.
- (sorts (

 ) ... (
) ... (

 )).
Subsorts of the new datatype. All these subsorts must be included
within the new base type. Thus, the enclosing sort of the first
subsort must be the new base type, and the enclosing sort of a later
subsort must be either the base type or a previously mentioned subsort
of it.
)).
Subsorts of the new datatype. All these subsorts must be included
within the new base type. Thus, the enclosing sort of the first
subsort must be the new base type, and the enclosing sort of a later
subsort must be either the base type or a previously mentioned subsort
of it.
- (atoms (

 ) ... (
) ... (

 )). Individual constants declared to
belong to the base type (or one of its subsorts).
)). Individual constants declared to
belong to the base type (or one of its subsorts).
- (constructors (
 (
(
 ...
...
 ) (selectors s1 ...sn-1))).
Function constants declared to construct elements of the new type (or
its subsorts). Each range sort must be the new base type or one of its
subsorts. Each domain sort may belong to the underlying theory, or
alternatively it may be the new base or one of its subsorts. It may
not be a higher sort involving the new type.
) (selectors s1 ...sn-1))).
Function constants declared to construct elements of the new type (or
its subsorts). Each range sort must be the new base type or one of its
subsorts. Each domain sort may belong to the underlying theory, or
alternatively it may be the new base or one of its subsorts. It may
not be a higher sort involving the new type.
- (sort-inclusions (

 ) ... (
) ... (

 )). Declare that every
element of subsort is also a member of supersort. This is
not needed when subsort is a syntactic subsort of supersort
in the sense that there are zero or more intermediate sorts
)). Declare that every
element of subsort is also a member of supersort. This is
not needed when subsort is a syntactic subsort of supersort
in the sense that there are zero or more intermediate sorts
 such that the enclosing sort of subsort is
such that the enclosing sort of subsort is
 ,
the enclosing sort of
,
the enclosing sort of  is supersort, and
the enclosing sort of
is supersort, and
the enclosing sort of  is
is
 for each i with
for each i with
 .
.
The purpose of the def-bnf form is to define a new recursive data type to
be added (as a conservative extension) to some existing theory. The members of
the new data type are the atoms in the declaration together with the objects
returned (``constructed'') by the constructor functions. We will use the
 to refer to the base type; symbols such as
to refer to the base type; symbols such as  will stand for any
sort included in the base type (such as the base sort
will stand for any
sort included in the base type (such as the base sort  itself);
itself);  will be used for any sort of the underlying theory.
will be used for any sort of the underlying theory.
The logical content of a data type definition of this kind is determined by two
main ideas:
- No Confusion. If c0 and c1 are two different constructor
functions, then the range of c0 is disjoint from the range of c1.
If a and b are two atoms, then
 .
Moreover
.
Moreover
 .
.
- No Junk. Everything in
 apart from the atoms is generated
by the constructor functions. This is in fact a form of induction. It
allows us to infer that a property holds of all members of the data
type on two assumptions:
apart from the atoms is generated
by the constructor functions. This is in fact a form of induction. It
allows us to infer that a property holds of all members of the data
type on two assumptions:
- 1.
- The property holds true of each atom;
- 2.
- The property holds true of a value returned by any constructor
function c, assuming that it holds true of those arguments that
belong to
 (rather than to some sort
(rather than to some sort 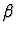 of the underlying
theory).
of the underlying
theory).
The implementation ensures that the resulting theory will be a model
conservative extension of the underlying theory. That is, given any model
M of the underlying theory, we can augment M with a new domain to
interpret  and provide interpretations of the new vocabulary so that
the resulting M' is a model of extended theory.
and provide interpretations of the new vocabulary so that
the resulting M' is a model of extended theory.
In the case where  contains no subtype, it is clear that to ensure
conservatism, it is enough to establish that
contains no subtype, it is clear that to ensure
conservatism, it is enough to establish that  will be non-empty. The
syntax of the declaration suffices to determine whether this condition is
met: either there must be an atom, or else at least one constructor function
must take all of its arguments from types
will be non-empty. The
syntax of the declaration suffices to determine whether this condition is
met: either there must be an atom, or else at least one constructor function
must take all of its arguments from types  of the underlying theory.
of the underlying theory.
If  does have subtypes, the implementation must establish that each
subtype is non-empty. That will hold if there is an ordering of the new
sorts
does have subtypes, the implementation must establish that each
subtype is non-empty. That will hold if there is an ordering of the new
sorts  such that, for each
such that, for each  ,
at least one of the
following conditions holds:
,
at least one of the
following conditions holds:
- 1.
- There is an atom declared to be of sort
 ;
or
;
or
- 2.
- There is a sort
 occurring earlier in the ordering, and
occurring earlier in the ordering, and
 is declared to be included within
is declared to be included within  ;
or
;
or
- 3.
- There is at least one constructor c declared with range sort
 ,
and every domain sort of c is either some
,
and every domain sort of c is either some  belonging to the underlying theory or some
belonging to the underlying theory or some  occurring
earlier in the ordering that
occurring
earlier in the ordering that  .
.
When this condition is not met, the implementation raises an error and
identifies the uninhabited sort (or sorts) for the user.
The BNF mechanism generates six categories
of axioms:
- Constructor definedness
- A constructor is well-defined for every
selection of arguments of the syntactically declared sorts.
- Disjointness
- If a and b are atoms and c0 and c1 are
constructors, then
 ,
,
 ,
and
,
and
 is disjoint from
is disjoint from
 .
.
- Selector/constructor
- If s is the
 th selector for the
constructor c, then
th selector for the
constructor c, then
 .
Moreover, if
.
Moreover, if
 ,
then
,
then
 for some
for some  .
.
- Sort Inclusions
-
 ,
when
,
when
 is specified as included within
is specified as included within  .
.
- Induction
- The type
 is the smallest containing the atoms and
closed under the constructor functions in the sense given above (``No
Junk'').
is the smallest containing the atoms and
closed under the constructor functions in the sense given above (``No
Junk'').
- Case Analysis
- If
 ,
where
,
where 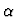 is the new type
or one of its subsorts, then one of the following holds:
is the new type
or one of its subsorts, then one of the following holds:
- 1.
- x is one of the atoms declared with sort
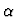 ;
;
- 2.
- x is in the range of some constructor declared with range
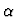 ;
;
- 3.
-
 ,
where either
,
where either 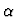 is the enclosing sort of
is the enclosing sort of
 ,
or else the inclusion of
,
or else the inclusion of  within
within 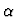 is
declared as a sort inclusion.
is
declared as a sort inclusion.
Strictly speaking this should be a theorem rather than an axiom, as
it follows from the induction principle.
A data type introduced via the BNF
mechanism justifies a schema for defining functions by primitive recursion.
Roughly speaking, a function g of sort
 is uniquely
determined if a sort
is uniquely
determined if a sort 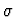 is given, together with the following:
is given, together with the following:
- For each atom, a value of sort
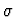 ;
;
- For each constructor c, with sort
a functional  of sort
of sort
is given. The primitive recursively defined function g will have the
property that
 is quasi-equal to
is quasi-equal to
Thus in effect  says how to combine the results of the
recursive calls (for arguments in the primary type) with the values
of the parameters (from sorts
says how to combine the results of the
recursive calls (for arguments in the primary type) with the values
of the parameters (from sorts  of the underlying theory).
of the underlying theory).
A number of consequences of the axioms are
installed.
The simplest example possible is:
(def-bnf nat
(theory pure-generic-theory-1)
(base-type nat)
(atoms (zero nat))
(constructors (succ (nat nat) (selectors pred))))
The axioms generated from this definition are displayed in
Figure 17.1 on page ![[*]](cross_ref_motif.gif) .
.
Figure 17.1:
Axioms for Nat, as Introduced by BNF
bnf data type nat:
 |
As a more complicated example, consider a programming language with phrases of
three kinds, namely identifiers, expressions, and statements. The data type to
be introduced corresponds to set of phrases of all three syntactic categories;
each syntactic category will be represented by a subsort. A BNF for the
language might take the form given in Figure 17.2, with x ranging
over numbers and s ranging over strings. A corresponding IMPS def form is
shown in Figure 17.3, where it is assumed that the underlying
theory String-theory contains a sort string representing
ASCII strings, as well as containing R.
Figure 17.2:
BNF Syntax for a Small Programming Language
|
|
Figure 17.3:
IMPS def-bnf Form for Programming Language Syntax
 |
def-cartesian-product
- name. A symbol to name the product sort.
- (
 .
sort-name is the name of a sort
.
sort-name is the name of a sort 
- (constructor constructor-name).
- (accessors
 .
.
- (theory theory-name). Required.
This form creates a new atomic sort 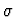 called name. This
sort can be regarded as the cartesian product of the sorts
called name. This
sort can be regarded as the cartesian product of the sorts
 The sort actually created is a subsort of the
function sort
The sort actually created is a subsort of the
function sort
- constructor-name is the name of the canonical
``n-tuple'' mapping:
-
 is the name of the canonical projection onto the
i-th coordinate:
is the name of the canonical projection onto the
i-th coordinate:

(def-cartesian-product complex
(rr rr)
(constructor make%complex)
(accessors real imaginary)
(theory h-o-real-arithmetic))
def-compound-macete
None.
This form adds a compound macete with the
given name and components. See the section on macetes for the
semantics of macetes.
(def-compound-macete FRACTIONAL-EXPRESSION-MANIPULATION
(repeat
beta-reduce
addition-of-fractions
multiplication-of-fractions
multiplication-of-fractions-left
multiplication-of-fractions-right
equality-of-fractions
left-denominator-removal-for-equalities
right-denominator-removal-for-equalities
strict-inequality-of-fractions
right-denominator-removal-for-strict-inequalities
left-denominator-removal-for-strict-inequalities
inequality-of-fractions
right-denominator-removal-for-inequalities
left-denominator-removal-for-inequalities))
(def-compound-macete ELIMINATE-IOTA-MACETE
(sequential
(sound
tr%abstraction-for-iota-body
beta-reduce
beta-reduce)
(series
tr%defined-iota-expression-elimination
tr%negated-defined-iota-expression-elimination
tr%left-iota-expression-equation-elimination
tr%right-iota-expression-equation-elimination)
beta-reduce))
def-constant
- constant-name. The name of the constant to be defined.
constant-name is also the name of the newly-built definition.
- defining-expr-string.
- (theory theory-name). Required.
- (sort sort-string).
- (usages
 .
.
This form creates a new constant c called
constant-name and a new axiom of the form c =e with usage
list
 ,
where e is
the expression specified by defining-expr-string. The sort
,
where e is
the expression specified by defining-expr-string. The sort
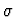 of c is the sort specified by sort-string if there
is a sort argument and otherwise is the sort of e. The new
constant and new axiom are added to the theory T named theory-name provided:
of c is the sort specified by sort-string if there
is a sort argument and otherwise is the sort of e. The new
constant and new axiom are added to the theory T named theory-name provided:
- constant-name is not the name of any current constant
of T or of a structural supertheory of T; and
- the formula
 is known to be a
theorem of T.
is known to be a
theorem of T.
(def-constant ABS
"lambda(r:rr, if(0<=r,r,-r))"
(theory h-o-real-arithmetic))
(def-constant >
"lambda(x,y:rr,y<x)"
(theory h-o-real-arithmetic)
(usages rewrite))
(def-constant POWER%OF%TWO
"lambda(x:zz,2^x)"
(sort "[zz,zz]")
(theory h-o-real-arithmetic))
def-imported-rewrite-rules
- (source-theory source-theory-name).
- (source-theories
 .
.
This form imports into the theory named
theory-name all the transportable rewrite rules installed in
the theory named source-theory-name (or in the theories named
 ).
).
def-inductor
- inductor-name.
- induction-principle. Can be a string representing the
induction principle in the current syntax or a name of a theorem.
- (theory theory-name). Required.
- (translation name). name is the name of a theory
interpretation. If this keyword is present, the formula used in
constructing the induction principle is actually the translation of
induction-principle.
- (base-case-hook name). name is the name of a macete
or a command.
- (induction-step-hook name). name is the name of a macete
or a command.
- (dont-unfold
 .
name is the name of a recursive constant in
the theory or the symbol
.
name is the name of a recursive constant in
the theory or the symbol #t. This form instructs the inductor not to
unfold the recursive constant named name when processing the
induction step. If #t is specified, then no recursive definitions will
be unfolded in the induction step.
The induction principle used for
constructing an inductor must satisfy a number of requirements.
This form builds an inductor from the
formula 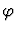 represented by induction-principle or if the
translation keyword is present, from the translation of
represented by induction-principle or if the
translation keyword is present, from the translation of
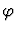 under the translation named by name. The base-case
and induction-step hooks are macetes or commands that provide additional
handling for the base and induction cases.
under the translation named by name. The base-case
and induction-step hooks are macetes or commands that provide additional
handling for the base and induction cases.
(def-inductor TRIVIAL-INTEGER-INDUCTOR
"forall(s:[zz,prop],m:zz,
forall(t:zz,m<=t implies s(t))
iff
(s(m) and
forall(t:zz,m<=t implies (s(t) implies s(t+1)))))"
(theory h-o-real-arithmetic))
(def-inductor NATURAL-NUMBER-INDUCTOR
"forall(s:[nn,prop],
forall(t:nn, s(t))
iff
(s(0) and forall(t:nn,s(t) implies s(t+1))))"
(theory h-o-real-arithmetic))
(def-inductor INTEGER-INDUCTOR
induct
(theory h-o-real-arithmetic)
(base-case-hook unfold-defined-constants-repeatedly))
(def-inductor SM-INDUCT
"forall(p:[state,prop],
forall(s:state, accessible(s) implies p(s))
iff
(forall(s:state, initial(s) implies p(s)) and
forall(s_1, s_2:state, a:action,
(accessible(s_1) and p(s_1) and tr(s_1, a, s_2))
implies
p(s_2))))"
(theory h-o-real-arithmetic)
(base-case-hook
eliminate-nonrecursive-definitions-and-simplify))
(def-inductor SEQUENCE-INDUCTOR
"forall(p:[[nn,ind_1],prop],
forall(s:[nn,ind_1], f_seq_q(s) implies p(s))
iff
(p(nil(ind_1)) and
forall(s:[nn,ind_1], e:ind_1,
f_seq_q(s) and p(s) implies p(cons{e,s}))))"
(theory sequences)
(base-case-hook simplify))
def-language
- (embedded-languages
 .
name is the name of a
language or theory.
.
name is the name of a
language or theory.
- (embedded-language name). name is the name of a
language or theory.
- (base-types
 .
.
- (sorts
 .
sort-spec is a list of the form
(sort enclosing-sort), called a sort-specification. sort must be a symbol, and
enclosing-sort must satisfy one of the following:
.
sort-spec is a list of the form
(sort enclosing-sort), called a sort-specification. sort must be a symbol, and
enclosing-sort must satisfy one of the following:
- It occurs in a previous sort specification.
- It is a sort in one of the embedded languages.
- It is a compound sort which can be built up from sorts of the
preceding kinds.
- (extensible
 .
type-sort-alist is a list of
the form (numerical-type-name sort). numerical-type-name is the name of a numerical type, that is, a
class of objects defined in T. For example, *integer-type* and
*rational-type* are names of numerical types. This keyword
argument is used for defining self-extending languages. This is a
language that incorporates new formal symbols when the expression
reader encounters numerical objects of the given type.
.
type-sort-alist is a list of
the form (numerical-type-name sort). numerical-type-name is the name of a numerical type, that is, a
class of objects defined in T. For example, *integer-type* and
*rational-type* are names of numerical types. This keyword
argument is used for defining self-extending languages. This is a
language that incorporates new formal symbols when the expression
reader encounters numerical objects of the given type.
- (constants
 .
constant-spec is a list
(constant-name sort-or-compound-sort).
.
constant-spec is a list
(constant-name sort-or-compound-sort).
This form builds a language with name
language-name satisfying the following properties:
- This language contains the sorts and constants
given by the sort and constant specification subforms.
- It contains the languages named
 as sublanguages.
as sublanguages.
- If the language contains the extensible keyword, then the
language may contain an infinite number of constants; these constants
are in one-to-one correspondence with elements of the numerical types
present in the type-sort-alist.
(def-language NUMERICAL-STRUCTURES
(extensible (*integer-type* zz) (*rational-type* qq))
(sorts (rr ind) (qq rr) (zz qq))
(constants
(^ (rr zz rr))
(+ (rr rr rr))
(* (rr rr rr))
(sub (rr rr rr))
(- (rr rr))
(/ (rr rr rr))
(<= (rr rr prop))
(< (rr rr prop))))
(def-language METRIC-SPACES-LANGUAGE
(embedded-language h-o-real-arithmetic)
(base-types pp)
(constants
(dist (pp pp rr))))
(def-language REAL-VECTOR-LANGUAGE
(embedded-language h-o-real-arithmetic)
(base-types uu)
(constants
(++ (uu uu uu))
(v0 uu)
(** (rr uu uu))))
(def-language HAM-SANDWICH-LANGUAGE
(base-types sandwich)
(embedded-language h-o-real-arithmetic)
(constants
(ham%sandwich sandwich)
(tuna%sandwich sandwich)
(refrigerator (sandwich unit%sort))))
def-order-processor
- (algebraic-processor name). The name of an algebraic
processor.
- (operations
 .
operation-alist is a
list of entries (operation-type operator), where operation-type is one of: <, <=. operator is the name of a
constant in the language of the associated algebraic processor.
.
operation-alist is a
list of entries (operation-type operator), where operation-type is one of: <, <=. operator is the name of a
constant in the language of the associated algebraic processor.
- (discrete-sorts
 .
.
This form builds an object called an order processor for simplification
of formulas involving order relations. Processors are used by IMPS to generate algebraic and order simplification procedures used by the
simplifier for the following purposes:
- To utilize theory-specific information of an algebraic nature in
performing simplification. For example, the expression x+x-x should
simplify to x, or x<x+1 should simplify to true.
- To reduce any formula built from formal constants whose value
can be algebraically computed from the values of the components. Thus
the expression 2<3 should reduce to true.
(def-order-processor RR-ORDER
(algebraic-processor rr-algebraic-processor)
(operations (< <) (<= <=))
(discrete-sorts zz))
def-primitive-recursive-constant
- constant name: The name of the function (or predicate) constant
to be introduced by the def-form.
- bnf: The BNF object furnishing the primitive
recursive schema for the definition (see def-bnf). The base type
of this BNF will also be the domain of the constant.
- (theory theory-name): Required. The theory to which the defined
constant will be added. This may be an extension of the theory of the
BNF with respect to which the recursion is performed.
- (range-sort range-sort-form): Required. This specifies the
range of the function or predicator being introduced; since the domain
will be the base sort of the BNF, this fixes the sort of the
constant.
- (atom-name value): Required, one for each
BNF atom. This specifies one base case of the recursive definition.
- (constructor-name var-names operator-body ): Required, one for each BNF constructor. This specifies one
recursive step of the recursive definition. The operator-body
specifies how the results of the recursive subcalls should be combined
(possibly with parameters not belonging to the datatype) to produce the
value of the recursive operator for an argument of this form.
Each BNF is automatically equipped with a
principle of definition by structural (primitive) recursion. A def-primitive-recursive-constant form instantiates this principle by
stipulating the intended range sort, the values for atoms of the BNF
data type, and how the recursively defined operator combines its results on
the arguments of each datatype constructor.
See, for instance, the compiler exercise file.
def-quasi-constructor
- name. The name of the quasi-constructor.
- lambda-expr-string.
- (language language-name). Required. language-name
may also be the name of a theory.
- (fixed-theories
 .
.
This form builds a quasi-constructor
named name from the schema specified by lambda-expr-string, which is a lambda-expression in the
language named language-name. The sorts in the theories named
 ,
...
,
...
 are
held fixed.
are
held fixed.
(def-quasi-constructor PREDICATE-TO-INDICATOR
"lambda(s:[uu,prop],
lambda(x:uu, if(s(x),an%individual, ?unit%sort)))"
(language indicators)
(fixed-theories the-kernel-theory))
(def-quasi-constructor GROUP
"lambda(a:sets[gg],
mul%:[gg,gg,gg],
e%:gg,
inv%:[gg,gg],
forall(x,y:gg,
(x in a and y in a) implies mul%(x,y) in a) and
e% in a and
forall(x:gg, x in gg% implies inv%(x) in gg%) and
forall(x:gg, x in a implies mul%(e%,x)=x) and
forall(x:gg, x in a implies mul%(x,e%)=x) and
forall(x:gg, x in a implies mul%(inv%(x),x)=e%) and
forall(x:gg, x in a implies mul%(x,inv%(x))=e%) and
forall(x,y,z:gg,
(x in a) and (y in a) and (z in a)
implies
mul%(mul%(x,y),z) = mul%(x,mul%(y,z))))"
(language groups))
def-record-theory
- theory-name. The name of a theory.
- (type symbol). Required.
- (accessors
 .
accessor-spec is a list
.
accessor-spec is a list
NO DESCRIPTION.
(def-record-theory ENTITIES-AND-LEVELS
(type access)
(accessors
(read "prop")
(write "prop")))
def-recursive-constant
- names. The name or lists of names of the constant or
constants to be defined.
- defining-functional-strings. A string or list of strings
specifying the defining functionals of the definition.
- (theory theory-name). Required.
- (usages
 .
.
- (definition-name def-name). The name of the definition.
Let T be the theory named theory-name;
 ,...,
,...,
 be the names given by names; and
be the names given by names; and
 be the functionals specified by the strings in defining-functional-strings. This form creates a list of new
constants
be the functionals specified by the strings in defining-functional-strings. This form creates a list of new
constants
 called
called
 ,...,
,...,
 and a set of new
axioms with usage list
and a set of new
axioms with usage list
 ,...,
,...,
 .
The axioms say that
.
The axioms say that
 are a minimal fixed
point of the family
are a minimal fixed
point of the family
 of functionals. The new
constants and new axioms are added to T provided:
of functionals. The new
constants and new axioms are added to T provided:
- each
 is not the name of any current
constant of T or of a structural supertheory of T; and
is not the name of any current
constant of T or of a structural supertheory of T; and
- each functional fi is known to be monotone in T.
If the definition-name keyword is present, the name of the
definition is def-name; otherwise, it is
 .
.
(def-recursive-constant SUM
"lambda(sigma:[zz,zz,[zz,rr],rr],
lambda(m,n:zz,f:[zz,rr],
if(m<=n,sigma(m,n-1,f)+f(n),0)))"
(theory h-o-real-arithmetic)
(definition-name sum))
(def-recursive-constant (EVEN ODD)
("lambda(even,odd:[nn,prop],
lambda(n:nn, if_form(n=0, truth, odd(n-1))))"
"lambda(even,odd:[nn,prop],
lambda(n:nn, if_form(n=0, falsehood, even(n-1))))")
(theory h-o-real-arithmetic)
(definition-name even-odd))
(def-recursive-constant OMEGA%EMBEDDING
"lambda(f:[nn,nn], a:sets[nn],
lambda(k:nn,
if(k=0,
iota(n:nn, n in a and
forall(m:nn, m<n implies not(m in a))),
lambda(z:nn,
iota(n:nn, n in a and z<n
forall(m:nn, (z<m and m<n) implies
(not(m in a)))))(f(k-1)))))"
(theory h-o-real-arithmetic)
(definition-name omega%embedding))
def-renamer
- name. A symbol naming the renamer.
- (pairs
 .
pair is of the form
(old-name new-name).
.
pair is of the form
(old-name new-name).
This form defines a T procedure named
name which, given a symbol x, returns the symbol y if (xy) is one of the pairs, and otherwise returns x.
(def-renamer SB-RENAMER
(pairs
(last%a%index last%b%index)
(a%inf b%inf)
(a%even b%even)
(a%odd b%odd)))
def-schematic-macete
- macete-name. A symbol naming the schematic macete.
- formula. A string representing the formula using the current syntax.
- null. The presence of this modifier means the macete is
nondirectional. This means that schematic macete which is built uses a
matching and substitution procedure which does not obey the variable
capturing protections and other restrictions of normal matching and
substitution.
- transportable. The presence of this modifier means the macete is transportable.
- (theory theory-language-name). Required. The name of
the language in which expression should be read in.
(def-schematic-macete ABSTRACTION-FOR-DIFF-PROD
"with(a,b:rr,y:rr,
diff(lambda(x:rr,a*b))(y)=
diff(lambda(x:rr,
lambda(x:rr,a)(x)*lambda(x:rr,b)(x)))(y))"
null
(theory calculus-theory))
def-script
- script-name. The name of the new command being created.
- N. The number of arguments required by the script.
- (
 .
A proof script consisting of 0 or more
forms.
.
A proof script consisting of 0 or more
forms.
- (retrieval-protocol proc). proc is the name of an
Emacs procedure which IMPS uses to interactively request command
arguments from the user. The default procedure is general-argument-retrieval-protocol which requires the user to supply
all the arguments in the minibuffer.
- (applicability-recognizer proc). proc is the name
of a T predicate or is the symbol
#t. The inclusion of this
argument will cause the command name to appear as a selection in the
command menu whenever the current sequent node satisfies the
predicate. Supplying #t as an argument is equivalent to
supplying a predicate which is always true.
This form is used to build a new command named script-name. This
new command can be used in either interactive mode or in script mode. The
script defining the command is a list of forms, each of which is a
command form or a keyword form. See a description of the
proof script language in Chapter 12.
(def-script EPSILON/N-ARGUMENT 1
((instantiate-universal-antecedent
"with(p:prop, forall(eps:rr, 0<eps implies p))" ($1))))
def-section
- (component-sections
 .
.
- (files
 .
.
This form builds a section which, when loaded, loads the sections with
names
 and then loads the files with specifications
and then loads the files with specifications
 .
A section can be
loaded with the form load-section.
.
A section can be
loaded with the form load-section.
(def-section BASIC-REAL-ARITHMETIC
(component-sections reals)
(files
(imps theories/reals/some-lemmas)
(imps theories/reals/arithmetic-macetes)
(imps theories/reals/number-theory)))
(def-section FUNDAMENTAL-COUNTING-THEOREM
(component-sections
basic-cardinality
basic-group-theory)
(files
(imps theories/groups/group-cardinality)
(imps theories/groups/counting-theorem)))
def-sublanguage
- (superlanguage superlanguage-name). Required.
The name of the language containing the sublanguage.
- (languages
 .
.
- (sorts
 .
.
- (constants
 .
.
This form finds the smallest sublanguage of the language L named
superlanguage-name which contains the sublanguages of Lnamed language-
 ,
..., language-
,
..., language-
 ;
the atomic sorts of L named sort-
;
the atomic sorts of L named sort-
 ,
..., sort-
,
..., sort-
 ;
and the constants of L named
;
and the constants of L named
 .
.
Each of
 may be the name of
a theory instead of a language.
may be the name of
a theory instead of a language.
(def-sublanguage REAL-VECTOR-LANGUAGE
(superlanguage vector-spaces-over-rr-language)
(languages h-o-real-arithmetic)
(sorts uu)
(constants ++ v0 **))
def-theorem
- name. The name of the theorem which may be ().
- formula-spec. A string representing the formula using the
current syntax or the name of a theorem.
- reverse.
- lemma. Not loaded when quick-loading.
- (theory theory-name). Required. The name of the theory
in which to install the theorem.
- (usages
 .
.
- (translation translation-name). The name of a theory
interpretation.
- (macete macete-name). The name of a bidirectional macete.
- (home-theory home-theory-name). The name of the home
theory of the formula specified by formula-spec.
- (proof proof-spec).
This form installs a theorem in three
steps. Let  be the theory interpretation named translation-name when there is a translation argument, and let
M be the bidirectional macete named macete-name when there is
a macete argument. Also, let T be the theory named theory-name, and let H be the theory named by home-theory-name. If there is no home-theory argument, then
H is the source theory of
be the theory interpretation named translation-name when there is a translation argument, and let
M be the bidirectional macete named macete-name when there is
a macete argument. Also, let T be the theory named theory-name, and let H be the theory named by home-theory-name. If there is no home-theory argument, then
H is the source theory of  if there is a translation
argument and otherwise H=T. Finally, let
if there is a translation
argument and otherwise H=T. Finally, let 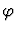 be the formula
specified by formula-spec in H.
be the formula
specified by formula-spec in H.
Step 1. IMPS verifies that 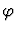 is a theorem of H.
If proof-spec is the symbol existing-theorem, IMPS checks to see that
is a theorem of H.
If proof-spec is the symbol existing-theorem, IMPS checks to see that 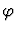 is alpha-equivalent to some existing
theorem of H. If the theorem is being installed in ``batch mode''
(see Section 12.3.1), IMPS verifies that
is alpha-equivalent to some existing
theorem of H. If the theorem is being installed in ``batch mode''
(see Section 12.3.1), IMPS verifies that 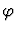 is a theorem of H by running the script proof-spec.
Otherwise, IMPS simply checks that
is a theorem of H by running the script proof-spec.
Otherwise, IMPS simply checks that 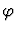 is a formula in H,
and it is assumed that the user has verified that
is a formula in H,
and it is assumed that the user has verified that 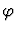 is a
theorem of H.
is a
theorem of H.
Step 2. The theorem  to be installed is generated from
to be installed is generated from
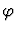 as follows:
as follows:
- If there is no translation or macete
argument and T=H, then
 .
.
- If there is no translation or macete
argument and T is a subtheory of H,
 is a formula of Twhich is the result of generalizing the constants of H which are not
in T (assuming each sort of T is also a sort of H).
is a formula of Twhich is the result of generalizing the constants of H which are not
in T (assuming each sort of T is also a sort of H).
- If there is a translation argument but no macete
argument, then
 is the translation of
is the translation of 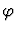 by
by  .
.
- If there is a macete argument but no translation
argument, then
 is the result of applying M to
is the result of applying M to 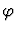 .
.
- If there is both a translation and macete argument,
then
 is the result of applying M to the translation of
is the result of applying M to the translation of
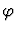 by
by  .
.
Step 3.  is installed as a theorem in T with usage
list
is installed as a theorem in T with usage
list
 ,
,
 ,
,
 .
.
If the modifier argument reverse is present, evaluating this
form is equivalent to evaluating the form without reverse
followed by evaluating the form again without reverse but with:
- name changed to the concatenation of rev% with
name, and
- formula-spec changed to a string which specifies
the ``reverse'' of the formula specified by formula-spec.
In other words, the reverse argument allows you to install both
a theorem and its reverse. It is very useful for building a macete
(or transportable macete) and its reverse by evaluating one form. Of
course, it would not be wise to use the reverse argument when
rewrite is a usage.
(def-theorem ABS-IS-TOTAL
"total_q(abs,[rr,rr])"
(theory h-o-real-arithmetic)
(usages d-r-convergence)
(proof
(
(unfold-single-defined-constant (0) abs)
insistent-direct-inference
beta-reduce-repeatedly
)))
(def-theorem RIGHT-CANCELLATION-LAW
left-cancellation-law
(theory groups)
(translation mul-reverse)
(proof existing theorem))
(def-theorem FUNDAMENTAL-COUNTING-THEOREM
"f_indic_q{gg%subgroup}
implies
f_card{gg%subgroup} =
f_card{stabilizer(zeta)}*f_card{orbit(zeta)}"
;; "forall(zeta:uu,
;; f_indic_q{gg%subgroup}
;; implies
;; f_card{gg%subgroup} =
;; f_card{stabilizer(zeta)}*f_card{orbit(zeta)})"
(theory group-actions)
(home-theory counting-theorem-theory))
def-theory
- (language language-name).
- (component-theories
 .
.
- (axioms
 .
axiom-spec is a list
.
axiom-spec is a list
where name, a symbol, is the optional name of the axiom and formula-string is a string representing the axiom in the syntax of
the language of the theory.
- (distinct-constants
 .
distinct is a list
.
distinct is a list
This form builds a theory named theory-name. The language of this theory is the union of the language
language-name and the languages of the component theories. The
axioms of the theory are the formulas represented by the strings in
the list axiom-spec. The distinct-constants list
implicitly adds new axioms asserting that the constants in each list
distinct are not equal.
(def-theory METRIC-SPACES
(component-theories h-o-real-arithmetic)
(language metric-spaces-language)
(axioms
(positivity-of-distance
"forall(x,y:pp, 0<=dist(x,y))"
transportable-macete)
(point-separation-for-distance
"forall(x,y:pp, x=y iff dist(x,y)=0)"
transportable-macete)
(symmetry-of-distance
"forall(x,y:pp, dist(x,y) = dist(y,x))"
transportable-macete)
(triangle-inequality-for-distance
"forall(x,y,z:pp, dist(x,z)<=dist(x,y)+dist(y,z))")))
(def-theory VECTOR-SPACES-OVER-RR
(language real-vector-language)
(component-theories generic-theory-1)
(axioms
("forall(x,y,z:uu, (x++y)++z=x++(y++z))")
("forall(x,y:uu, x++y=y++x)")
("forall(x:uu, x++v0=x)")
("forall(x,y:rr, z:uu, (x*y)**z=x**(y**z))")
("forall(x,y:uu,a:rr,a**(x++y)=(a**x)++(a**y))")
("forall(a,b:rr, x:uu,(a+b)**x=(a**x)++(b**x))")
("forall(x:uu, 0**x=v0)")
("forall(x:uu, 1**x=x)")))
def-theory-ensemble
- ensemble-name. The name of the theory ensemble. This will also
be the name of the base theory unless the base-theory
keyword argument is provided.
- (base-theory theory-name) theory-name is the name
of the base theory of the ensemble. If this keyword argument is not
included then the base theory is that theory with the name
ensemble-name.
- (fixed-theories
 .
The theories listed are not
replicated when the theory replicas and multiples are built. If this
argument is not provided, then the fixed theories are those in the
global fixed theories list at the time the form is evaluated.
.
The theories listed are not
replicated when the theory replicas and multiples are built. If this
argument is not provided, then the fixed theories are those in the
global fixed theories list at the time the form is evaluated.
- (replica-renamer proc-name). proc-name is the name
of a procedure of one integer argument, used to name sorts and
constants of theory replicas. The default procedure is to subscript
the corresponding sort and constant of the base theory.
This form builds a theory ensemble such
that
- 1.
- The base theory is the theory with name theory-name if the base-theory keyword argument is provided or ensemble-name
otherwise.
- 2.
- The fixed theories are those given in the fixed-theories keyword
argument list if the fixed-theories keyword argument is provided
or those theories in the global fixed theories list at the time the
form is evaluated.
If there is already a theory ensemble with
name ensemble-name but with different fixed-theories set or
different renamer an error will result.
(def-theory-ensemble METRIC-SPACES)
def-theory-ensemble-instances
- ensemble-name. An error will result if no ensemble exists
with ensemble-name.
This form is used to build translations
from selected theory multiples and to transport natively defined
constants and sorts from these multiples. To describe the
effects of evaluating this form, we consider a number of cases and
subcases determined by the presence of certain keyword arguments.
- (target-theories
 .
Let
.
Let
 be the theory with
name
be the theory with
name
 In this case, evaluation of the form builds
translations and transports natively defined constants and sorts by
these translations from selected theory multiples into the theory
union
In this case, evaluation of the form builds
translations and transports natively defined constants and sorts by
these translations from selected theory multiples into the theory
union
The theory multiples
that are selected as translation source theories are determined by the
multiples or permutations keyword arguments as follows:
- (target-multiple n). This case can be reduced to
the case of the (target-theories
 argument by letting
argument by letting
 be the name of the i-th theory replica.
be the name of the i-th theory replica.
(def-theory-ensemble-instances METRIC-SPACES
(target-theories h-o-real-arithmetic metric-spaces)
(multiples 1 2)
(sorts (pp rr pp))
(constants (dist "lambda(x,y:rr,abs(x-y))" dist)))
def-theory-ensemble-multiple
- ensemble-name. An error will result if no ensemble exists
with ensemble-name.
- N. An integer.
Builds a theory which is an N-multiple
of the theory ensemble base, together with N theory
interpretations from the base theory into the multiple. All
existing definitions of the base theory are translated via these
interpretations. The N-multiple is constructed to be a subtheory
of the (N+1)-multiple.
(def-theory-ensemble-multiple metric-spaces 2)
def-theory-ensemble-overloadings
- ensemble-name. An error will result if no ensemble exists
with ensemble-name.
-
 Each N is an integer
Each N is an integer
Installs overloadings for constants
natively defined in the theory multiples

(def-theory-ensemble-overloadings metric-spaces 1 2)
def-theory-instance
- name. The name of the theory to be created.
- (source source-theory-name). Required.
- (target target-theory-name). Required.
- (translation trans-name). Required.
- (fixed-theories
 .
.
- (renamer renamer). Name of a renaming procedure.
- (new-translation-name new-trans-name). Name of the
the translation to be created.
Let T0 and
 be
the source and target theories, respectively, of the translation
be
the source and target theories, respectively, of the translation
 named trans-name. Also, let T1 and
named trans-name. Also, let T1 and
 be the theories named source-theory-name and target-theory-name, respectively. Lastly, let
be the theories named source-theory-name and target-theory-name, respectively. Lastly, let
 be the set of
theories named
be the set of
theories named
 .
.
Suppose that T0 and
 are subtheories of T1 and
are subtheories of T1 and
 ,
respectively, and that every member of
,
respectively, and that every member of
 is a
subtheory of T1. The theory named name is an extension Uof
is a
subtheory of T1. The theory named name is an extension Uof
 built as follows. First, the primitive vocabulary
of T1 which is outside of T0 and
built as follows. First, the primitive vocabulary
of T1 which is outside of T0 and
 is added to the language
of
is added to the language
of
 ;
the vocabulary is renamed using the value of renamer. Next, the translations of the axioms of T1 which are
outside of T0 and
;
the vocabulary is renamed using the value of renamer. Next, the translations of the axioms of T1 which are
outside of T0 and
 are added to the axioms of
are added to the axioms of
 ;
the axioms are renamed using the value of renamer. U is union of the resulting theory and the members of
;
the axioms are renamed using the value of renamer. U is union of the resulting theory and the members of
 . The translation
. The translation  from T1 to U extending
from T1 to U extending  is
created with name new-trans-name.
is
created with name new-trans-name.
(def-theory-instance METRIC-SPACES-COPY
(source metric-spaces)
(target the-kernel-theory)
(translation the-kernel-translation)
(fixed-theories h-o-real-arithmetic))
(def-theory-instance VECTOR-SPACES-OVER-RR
(source vector-spaces)
(target h-o-real-arithmetic)
(translation fields-to-rr)
(renamer vs-renamer))
def-theory-processors
- (algebraic-simplifier
 .
.
Each entry spec
is a list
where processor-name is the name of an algebraic processor and
are constant names denoting functions. We will say that the operators
 are within the scope of the specified processor.
are within the scope of the specified processor.
- (algebraic-order-simplifier
 .
.
Each spec
is a list
where processor-name is the name of an order processor and
are constant names denoting two-place predicates. We will say that
the predicates
 are within the scope of the
specified order processor.
are within the scope of the
specified order processor.
- (algebraic-term-comparator
 .
spec is just
the name of an algebraic or order processor. We will
say that the equality constructor is within the scope of the specified
processor.
.
spec is just
the name of an algebraic or order processor. We will
say that the equality constructor is within the scope of the specified
processor.
This form causes the simplifier of the theory named theory-name
to simplify certain terms using the specified algebraic and order
processors as follows:
- All applications of an operator or predicate within the scope
of a processor are handled by that processor. An operation or
predicate may be within the scope of more than one processor.
- All equalities are handled by processors which contain the
equality constructor within its scope.
(def-theory-processors H-O-REAL-ARITHMETIC
(algebraic-simplifier
(rr-algebraic-processor * ^ + - / sub))
(algebraic-order-simplifier (rr-order < <=))
(algebraic-term-comparator rr-order))
(def-theory-processors VECTOR-SPACES-OVER-RR
(algebraic-simplifier
(vector-space-algebraic-processor ** ++))
(algebraic-term-comparator
vector-space-algebraic-processor))
def-translation
- name: The name of the translation.
- force.
- force-under-quick-load.
- dont-enrich.
- (source source-theory-name). Required.
- (target target-theory-name). Required.
- (assumptions
 .
.
- (fixed-theories
 .
.
- (sort-pairs
 .
.
Each
sort-pair-spec has one of the following forms:
- (sort-name sort-name).
- (sort-name sort-string).
- (sort-name (pred expr-string)).
- (sort-name (indic expr-string)).
- (constant-pairs
 ,
where
,
where
const-pair-spec has one of the following forms:
- (constant-name constant-name).
- (constant-name expr-string).
- (core-translation core-translation-name). The name of a
theory interpretation.
- (theory-interpretation-check check-method).
This form builds a translation named name from the source theory S named source-theory-name to
the target theory T named target-theory-name. (The target
context in T is the set of assumptions specified by
 ,
,
 ,
,
 .) The
translation is specified by the set of fixed theories, the set of sort
pairs, and the set of constant pairs.
.) The
translation is specified by the set of fixed theories, the set of sort
pairs, and the set of constant pairs.
If there is a core-translation argument, an extension of the
translation named core-translation-name is build using the
information given by the other arguments. The argument theory-interpretation-check tells IMPS how to check if the
translation is a theory interpretation (relative to the set of
assumptions).
If the modifier argument force is present, the obligations of
the translation are not generated, and thereby the translation is
forced to be a theory interpretation. Similarly, if the modifier
argument force-under-quick-load is present and the switch quick-load? is set to true, the obligations of the translation are
not generated. The former lets you build a theory interpretation when
the obligations are very hard to prove, and the latter is useful for
processing the def-form faster, when it has been previously determined
that the translation is indeed a theory interpretation.
If the modifier argument dont-enrich is present, the translation
will not be enriched. A translation is enriched at various times to
take into account new definitions in the source and target theories.
If one expects there to be many untranslated definitions after
enrichment, it may be computationally beneficial to use this modifier
argument.
(def-translation MONOID-THEORY-TO-ADDITIVE-RR
(source monoid-theory)
(target h-o-real-arithmetic)
(fixed-theories h-o-real-arithmetic)
(sort-pairs
(uu rr))
(constant-pairs
(e 0)
(** +))
(theory-interpretation-check using-simplification))
(def-translation MUL-REVERSE
(source groups)
(target groups)
(fixed-theories h-o-real-arithmetic)
(constant-pairs
(mul "lambda(x,y:gg, y mul x)"))
(theory-interpretation-check using-simplification))
(def-translation GROUPS->SUBGROUP
force
(source groups)
(target groups)
(assumptions
"with(a:sets[gg], nonempty_indic_q{a})"
"with(a:sets[gg],
forall(g,h:gg,
(g in a) and (h in a)
implies
(g mul h) in a))"
"with(a:sets[gg],
forall(g:gg, (g in a) implies (inv(g) in a)))")
(fixed-theories h-o-real-arithmetic)
(sort-pairs
(gg (indic "with(a:sets[gg], a)")))
(constant-pairs
(mul "with(a:sets[gg],
lambda(x,y:gg,
if((x in a) and (y in a), x mul y, ?gg)))")
(inv "with(a:sets[gg],
lambda(x:gg, if(x in a, inv(x), ?gg)))"))
(theory-interpretation-check using-simplification))
def-transported-symbols
- names. The name or lists of names of defined atomic
sorts and constants to be transported.
- (translation translation-name). Required.
- (renamer renamer.) Name of a renaming procedure.
Let T and T' be the source and
target theories, respectively, of the translation  named translation-name, and let
named translation-name, and let
 ,...,
,...,
 be the symbols whose names are given by names. For each
be the symbols whose names are given by names. For each
 which is a defined symbol in T, this form creates
a corresponding new defined symbol
which is a defined symbol in T, this form creates
a corresponding new defined symbol
 in
T' by translating the defining object of
in
T' by translating the defining object of
 via
via
 .
If
.
If  already translates
already translates
 to some
defined symbol, the new symbol is not created.
to some
defined symbol, the new symbol is not created.
(def-transported-symbols
(last%a%index a%inf a%even a%odd)
(translation schroeder-bernstein-symmetry)
(renamer sb-renamer))
(def-transported-symbols
(prec%increasing prec%majorizes prec%sup)
(translation order-reverse)
(renamer first-renamer))
def-overloading
- symbol. A symbol to overload (that is, to have multiple
meanings which are determined by context.)
-
 theory-name-pair is a list (theory-name symbol-name).
theory-name-pair is a list (theory-name symbol-name).
(def-overloading *
(h-o-real-arithmetic *)
(normed-linear-spaces **))
def-parse-syntax
- constant-name. This is a symbol or a list of symbols.
- (token spec). spec is a symbol or a string. If this
argument is omitted, by default it is constant-name.
- (left-method proc-name). proc-name is the name of a
procedure for left parsing of the token.
- (null-method proc-name). proc-name is the name of a
procedure for null parsing of the token.
- (table table-name). table-name is the name of the
parse-table being changed. If this argument is omitted, the default value
is the global parse table *parse*.
- (binding N). Required. N is the binding or
precedence of the token.
This form allows you to set (or reset)
the parse syntax of a constant. In particular, you can change the
precedence, parsing method, and token representation of a constant.
The most common parsing methods are:
- infix-operator-method. For example multiplication and addition use this method.
- prefix-operator-method. comb, the binomial coefficient
function, uses this method.
- postfix-operator-method. ! uses this method.
Note that an operator can have both a null-method and a left-method.
(def-parse-syntax +
(left-method infix-operator-method)
(binding 100))
(def-parse-syntax factorial
(token !)
(left-method postfix-operator-method)
(binding 160))
def-print-syntax
- constant-name. This is a symbol.
- tex. If this argument is present, then the syntax is added
to the global TEX print table.
- (token spec). spec is a symbol, a string or a list
of such. If this argument is omitted, by default it is constant-name.
- (method proc-name). proc-name is the name of a
procedure for printing of the token.
- (table table-name). table-name is the name of the
parse-table being changed. If this argument is omitted, and the tex modifier argument is not given, the default value is the global
print table *form*.
- (binding N). Required. N is the binding or
precedence of the token.
This form allows you to set (or reset)
the print syntax of a constant. In particular, you can change the
precedence, parsing method, and token representation of a constant.
(def-print-syntax +
(method present-binary-infix-operator)
(binding 100))
(def-print-syntax factorial
(token !)
(method present-postfix-operator)
(binding 160))
load-section
- reload. Causes the section to be reloaded if
the section has already been loaded.
- reload-files-only. Causes the files of the section (but
not the component sections) to be reloaded if the section has already
been loaded.
- quick-load. Causes the section to be quick-loaded.
None.
If there are no modifier arguments, this
form will simply load the component sections and files of the section
named section-name which have not been loaded.
include-files
None.
- reload. Causes a file to be reloaded if
the file has already been loaded.
- quick-load. Causes the files to be quick-loaded.
- (files
 .
.
If there are no modifier arguments, this
form will simply load the files with specifications
 which have not been
loaded.
which have not been
loaded.
view-expr
- expression-string. A string representing the expression to
be built and viewed.
- fully-parenthesize. Causes the expression to be viewed
fully parenthesized.
- fully. Same as fully-parenthesize.
- no-quasi-constructors. Causes the expression to be
viewed without quasi-constructor abbreviations.
- no-qcs. Same as no-quasi-constructors.
- tex. Causes the expression to be xviewed (i.e., printed
in TEX and displayed in an X window TEX previewer).
- (language language-name). language-name is the name of a
language or theory in which to build the expression.



Next: 18. The Proof Commands
Up: 3. Reference Manual
Previous: 3. Reference Manual
System Administrator
2000-07-23
 .
.
![[*]](cross_ref_motif.gif) .
.


