


Next: 15. The Iota Constructor
Up: 2. User's Guide
Previous: 13. Simplification
Subsections
14. Macetes
In addition to its simplifier, IMPS also provides a separate
mechanism for manipulating formal expressions by applying theorems.
Unlike simplification, it is under the control of the user. The basic
idea is that some expression manipulation procedures--for instance,
conditional rewrite rules--are in fact direct applications of
theorems. Other expression manipulation procedures can be formed from
existing ones using a simple combination language. These expression
manipulation procedures are called macetes.14.1 Formally, a macete
is a function M which takes as arguments a context 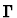 and an
expression e (called the source expression) and returns
another expression
and an
expression e (called the source expression) and returns
another expression
 (called the replacement expression).
In general, the replacement expression does not have to be equal to
the source expression.
(called the replacement expression).
In general, the replacement expression does not have to be equal to
the source expression.
Macetes serve
two somewhat different purposes:
- They are a straightforward way to apply a theorem or a
collection of theorems to a sequent in a deduction graph.
- They are also a mechanism for computing with theorems.
A macete can be atomic or compound. Compound macetes are
obtained by applying a macete constructor to a list of one or
more macetes.
Atomic macetes are classified as:
- Schematic macetes. A schematic macete is one in which the
replacement expression is obtained from the source expression by matching
and substitution. Schematic macetes can be thought of as conditional rewrite rules.
- Procedural macetes. These are macetes which compute the
replacement expression by a more complicated procedure. There are only a
few such procedures:
- simplify
- beta-reduce
- beta-reduce-insistently
Having these procedures as macetes allows you to build more powerful
and useful compound macetes.
Macetes can be also classified according to the relation between the
source and replacement expressions.
- Bidirectional. Whatever the context and source expression, the replacement
expression is quasi-equal to the source expression, that is, given any
legitimate model in which the context assumptions are true, either
both source expression and replacement expression have no value or
their value is identical.
- Backward-directional. Whatever the context and source expression, the replacement
expression is quasi-equal to or implies the source expression. Notice
that implication only makes sense for formulas of sort

- Nondirectional. There are contexts and source
expressions in which the target expression is neither quasi-equal to
nor implies the source expression.
A schematic macete can be associated to any formula in two ways
depending on the kind of matching procedure used. IMPS has two
general forms of matching called expression matching and translation matching.
Let us consider first the case of expression matching. To any IMPS formula we can associate:
- A source pattern. This is an expression s.
- A replacement pattern. This is an expression r.
- A list of condition patterns. This is a list of expressions

- A direction specifier: this specifier can be either bidirectional or backward-directional.
Suppose the formula is
 where
where 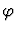 itself is not a universal
formula. The patterns are extracted from
itself is not a universal
formula. The patterns are extracted from 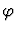 depending on the form
of
depending on the form
of 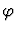 as described by the following table:
as described by the following table:
| Form |
Source |
Replacement |
Conditions |
Spec. |
 |
t1 |
t2 |
 |
Bid. |
 |
t1 |
t2 |
 |
Bid. |
 |
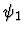 |
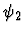 |
 |
Bid. |
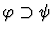 |
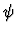 |
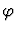 |
None |
Back. |
 |
t1 |
t2 |
None |
Bid. |
 |
t1 |
t2 |
None |
Bid. |
 |
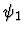 |
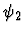 |
None |
Bid. |
 |
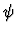 |
 |
None |
Bid. |
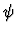 |
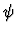 |
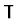 |
None |
Bid. |
Notes
We now describe how a schematic macete M is obtained from the
source, replacement, condition patterns, and direction specifier of a
formula. Given a context 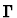 and an expression t, the result of
applying M to
and an expression t, the result of
applying M to 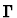 and t is determined as follows: Let
and t is determined as follows: Let  be the set of paths
be the set of paths
 to subexpressions elof t which satisfy all of the following conditions:
to subexpressions elof t which satisfy all of the following conditions:
- If the directional specifier is backward-directional, the parity of lmust be +1; otherwise, no condition is imposed on the path.
- The source pattern s matches el. Thus there is a substitution
 such that
such that  applied to s gives el.
applied to s gives el.
- The validity of all the convergence requirements of the substitution
 and all the formulas
and all the formulas
 in the context
in the context 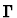 localized at the path l are called
the minor premises generated by the macete application.
These formulas may or may not generate applicability conditions:
localized at the path l are called
the minor premises generated by the macete application.
These formulas may or may not generate applicability conditions:
- If the macete is being applied with the
accumulation of minor premises, then these formulas are posted as new
sequents and must be proven separately. No new applicability
conditions are generated in this case.
- Otherwise, the minor premises must be recognized as valid by the
simplifier.
- No smaller path
 satisfies the preceding conditions.
satisfies the preceding conditions.
The replacement formula is obtained by replacing each subexpression
el by
 Macetes obtained in this way are called elementary macetes.
Macetes obtained in this way are called elementary macetes.
Whenever you enter a theorem into a theory, the associated schematic
macete is automatically installed, so that you can use it in
deductions by hitting the key m.
The case of translation matching is similar, but instead of
considering only convergence requirements, we need to insure that the
translation component of the translation match is a theory
interpretation. Macetes obtained in this way are called transportable macetes. The use of a theorem as a transportable macete
must be entered into its usage list when the theorem is entered.
Frequently it is useful to construct a schematic macete from an
arbitrary formula by using a matching and substitution procedure which
does not obey the variable capturing protections and other
restrictions of normal matching. We refer to this as nullary
matching and substitution. For instance, to apply a theorem which
involves quantification over functions, one often has to build a
lambda-abstraction of a sub-expression. We shall see later on how this
can be done.
Compound macetes are built from atomic macetes and other compound
macetes using macete constructors. The constructors are:
Now whether the resulting macete is bidirectional or
backward-directional, can be determined by considering the
bidirectionality or backward-directionality each of the
components.
- Series, sequential, parallel, repeat, and without-minor-premises
macete constructors: If all the Mi are bidirectional macetes then
the compound macete
is bidirectional. Similarly, if all the arguments Mi are
backward-directional macetes then the compound macete is also
backward-directional.
- Sound macete constructor: If M2,M3 are bidirectional, then
the compound macete
is always
bidirectional, regardless of M1. If M2 is backward-directional
and M3 is bidirectional, then the compound macete is
backward-directional. In all other cases, the compound macete is
nondirectional.
Schematic macetes are for the most part installed by the system when
theorems installed.
- 1.
- Elementary macetes are automatically installed when a theorem
is added to a theory. The name of the installed macete is the same as
the name of the theorem which generates it.
- 2.
- Transportable macetes are installed when the transportable-macete
modifier is present in the usage list of a theorem or axiom. Moreover,
in this case, the name of the installed macete is the name of theorem
which generates it with the prefix tr%.
Macetes are also automatically built when atomic sort and constant
definitions are made by the user.
- 1.
- For directly defined constants, the macete corresponding to
the constant defining equation is installed. This macete is named
constant-name-equation_theory-name.
If the usage list of the definition includes the rewrite
modifier and the defined constant is a function, the constant defining
equation in applied form is also include as a macete named
constant-name-applied-equation_theory-name.
- 2.
- For recursively defined constants, a number of macetes are installed:
- (a)
- The equation axioms named
constant-name-equation_theory-name
- (b)
- The minimality axiom named
definition-name-strong-minimality_theory-name
- (c)
- The minimality theorem named
definition-name-minimality_theory-name
- 3.
- For defined atomic sorts a number of macetes are installed:
- (a)
- The sort defining axiom named
sort-name-defining-axiom_theory-name.
- (b)
- Some auxiliary theorems named
sort-name-in-quasi-sort_theory-name
and
sort-name-in-quasi-sort-domain_theory-name
Nondirectional schematic macetes usually are not associated to
theorems. The form def-schematic-macete can be used for
building schematic macetes of all kinds. You can build compound macetes
using the form def-compound-macete.
A macete is ``applicable'' to a formula if applying the macete
modifies the formula in some way. The only sure-fire way of
determining whether a macete is applicable, is to actually apply the
macete and see the result. However, there are simple heuristic
conditions which can be used to quickly determine that some macetes
are not applicable. For example, for an elementary bidirectional
macete, if the left hand side of the macete does not match any
subexpression of the formula, then clearly the macete it is not
applicable. For transportable macetes other similar inapplicability
conditions are used. Macetes are tabulated in such a way that it is
possible to quickly throw out inapplicable ones using these heuristic
conditions. IMPS exploits this to provide users with a dynamic help
facility for selecting macetes. The use of this facility is explained
more extensively in Chapter 4.
- 1.
- Conceptually the macete mechanism is extremely simple.
Users however, should not underestimate its power, usefulness, and
flexibility. The utility of macetes hinges on three facts:
- The way a theorem is converted into a macete depends on the syntactic form of the
the theorem as explained earlier in this section. In particular, it is
important that theorems which are implications can be used as macetes
along with those that are conditional equalities. Moreover, the
``conversion algorithm'' is based on a number of heuristics that in
our experience work very well.
- Macetes can be combined using macete constructors. It has been our experience that
carefully building a collection of compound macetes is an important
part of developing a theory.
- Macetes are tabulated in such a way that the macetes which are applicable
to a given formula can be retrieved very effectively and displayed to
the user in a menu. In situations where over 500 macetes are
installed, the menu usually contains less than twenty entries and
takes less than ten seconds to compute.
- 2.
- Though there are various modes of applying macetes, the default mode,
with minor premises, is the one you want to use in most cases.
The without-minor-premises macete constructor is often useful for
building compound macetes to be used in this mode.



Next: 15. The Iota Constructor
Up: 2. User's Guide
Previous: 13. Simplification
System Administrator
2000-07-23
![]() and an
expression e (called the source expression) and returns
another expression
and an
expression e (called the source expression) and returns
another expression
![]() (called the replacement expression).
In general, the replacement expression does not have to be equal to
the source expression.
(called the replacement expression).
In general, the replacement expression does not have to be equal to
the source expression.
![]() and an expression t, the result of
applying M to
and an expression t, the result of
applying M to ![]() and t is determined as follows: Let
and t is determined as follows: Let ![]() be the set of paths
be the set of paths
![]() to subexpressions elof t which satisfy all of the following conditions:
to subexpressions elof t which satisfy all of the following conditions: