The logic of IMPS is called LUTINS7.1, a Logic of Undefined Terms for Inference in a Natural Style. LUTINS is a kind of predicate logic that is intended to support standard mathematical reasoning. It is classical in the sense that it allows nonconstructive reasoning, but it is nonclassical in the sense that terms may be nondenoting. The logic, however, is bivalent; formulas are always defined.
Unlike first-order predicate logic, LUTINS provides strong support for specifying and reasoning about partial functions (i.e., functions which are not necessarily defined on all arguments), including the following mechanisms:
The treatment of partial functions in LUTINS is studied in [4], while the treatment of subtypes is the subject of [5]. In this chapter we give a brief overview of LUTINS. For a detailed presentation of LUTINS, see [16]7.2.
A LUTINS language contains two kinds of objects: sorts and expressions. Sorts denote nonempty domains of elements (mathematical objects), while expressions denote members of these domains. Expressions are used for both referring to elements and making statements about them.
In this section we give a brief description of a hypothetical language
![]() . This language will be presented using the ``mathematical
syntax'' which will be used throughout the rest of the manual. There
are other syntaxes for LUTINS, including the ``string
syntax'' introduced in Chapter 3 and the
``s-expression syntax'' presented in [16].
. This language will be presented using the ``mathematical
syntax'' which will be used throughout the rest of the manual. There
are other syntaxes for LUTINS, including the ``string
syntax'' introduced in Chapter 3 and the
``s-expression syntax'' presented in [16].
Expressions are formed by applying constructors to variables, constants, and compound expressions. The constructors are given in Table 7.1; they serve as ``logical constants'' that are available in every language. Variables and constants belong to specific languages.
|
In the mathematical syntax, the symbols for the constructors, the common punctuation symbols, and the symbol with are reserved. By a name, we mean any unreserved symbol.
The sorts of
![]() are generated from a finite set
are generated from a finite set
![]() of names called
atomic sorts. More precisely, a sort of
of names called
atomic sorts. More precisely, a sort of
![]() is a sequence of symbols defined inductively by:
is a sequence of symbols defined inductively by:
![]() assigns each
assigns each
![]() a member of
a member of
![]() called the
enclosing sort of
called the
enclosing sort of ![]() .
The atomic/enclosing sort
relation determines a partial order
.
The atomic/enclosing sort
relation determines a partial order ![]() on
on
![]() with the
following properties:
with the
following properties:
The members of
![]() which are maximal with respect to
which are maximal with respect to ![]() are
called types. A base type is a type which is atomic.
Every language has the base type
are
called types. A base type is a type which is atomic.
Every language has the base type ![]() which denotes the set
which denotes the set
![]() of standard truth values. The type of a sort
of standard truth values. The type of a sort ![]() ,
written
,
written
![]() ,
is the unique type
,
is the unique type
![]() such that
such that
![]() .
The least upper
bound of
.
The least upper
bound of ![]() and
and ![]() ,
written
,
written
![]() ,
is the least upper bound of
,
is the least upper bound of ![]() and
and ![]() in the
partial order
in the
partial order ![]() .
(The least upper bound of two sorts with the
same type is always defined).
.
(The least upper bound of two sorts with the
same type is always defined).
A function sort is a sort ![]() such that
such that
![]() has
the form
has
the form
![]() .
The
range sort of a function sort
.
The
range sort of a function sort ![]() ,
written
,
written
![]() ,
is defined as follows: if
,
is defined as follows: if
![]() ,
then
,
then
![]() ;
otherwise,
;
otherwise,
![]() where
where ![]() is the
enclosing sort of
is the
enclosing sort of ![]() .
.
Sorts are divided into two kinds as follows: A sort is of kind
![]() if either it is
if either it is ![]() or it is a compound sort
or it is a compound sort
![]() where
where
![]() is of kind
is of kind
![]() ;
otherwise it is of kind
;
otherwise it is of kind ![]() .
We shall see later
the purpose behind this division. All atomic sorts except
.
We shall see later
the purpose behind this division. All atomic sorts except ![]() are
of kind
are
of kind ![]() .
.
![]() contains a set
contains a set
![]() of names called constants.
Each constant is assigned a sort in
of names called constants.
Each constant is assigned a sort in
![]() . An expression of
. An expression of
![]() of sort
of sort ![]() is a sequence of symbols defined inductively by:
is a sequence of symbols defined inductively by:
Expressions will usually be written in an abbreviated form as follows.
Suppose A is an expression whose free variables are
![]() .
Then A is
abbreviated as
.
Then A is
abbreviated as
Parentheses in expressions may be suppressed when meaning is not lost. In addition, the following alternate notation may be used in the IMPS mathematical syntax:
The semantics for a LUTINS language is defined in terms of
models that are similar to models of many-sorted first-order logic.
Let
![]() be a LUTINS language, and let
be a LUTINS language, and let
![]() denote the
set of sorts of
denote the
set of sorts of
![]() .
.
A frame for
![]() is a set
is a set
![]() of nonempty domains (sets) such that:
of nonempty domains (sets) such that:
A model for
![]() is a pair
is a pair
![]() where
where
![]() is a frame for
is a frame for
![]() and I is a function which maps each constant of
and I is a function which maps each constant of
![]() of sort
of sort ![]() to an element of
to an element of
![]() .
.
Let
![]() be a model for
be a model for
![]() . A variable
assignment into
. A variable
assignment into
![]() is a function which maps each variable
is a function which maps each variable
![]() of
of
![]() to an element of
to an element of
![]() .
Given a
variable assignment
.
Given a
variable assignment ![]() into
into
![]() ; distinct variables
; distinct variables
![]() ;
and
;
and
![]() ,
,
let
,
,
let
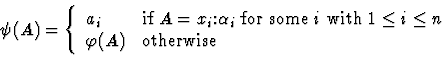
![]() is the partial binary function on variable assignments
into
is the partial binary function on variable assignments
into
![]() and expressions of
and expressions of
![]() defined by the following statements:
defined by the following statements:
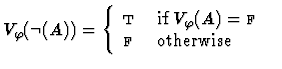
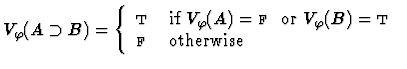
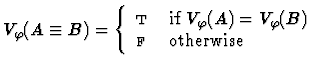
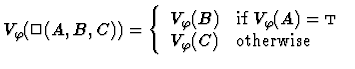
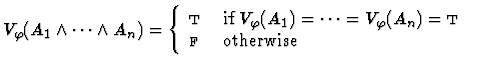
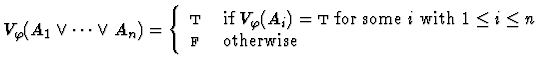
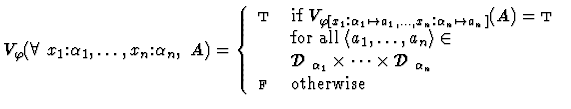
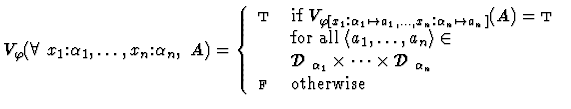
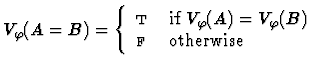
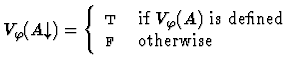
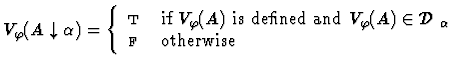
Clearly, for each variable assignment ![]() into
into
![]() and each
expression A of
and each
expression A of
![]() ,
,
The logic can be effectively extended by introducing ``quasi-constructors.'' They are the subject of Chapter 10.
% is often used in the names of variables
and constants in the string syntax to denote a space (the character
_ is used to denote the start of a subscript). This character
is printed in the mathematics syntax as either % or _.